Access to technology and foundational math proficiency among students: empirical evidence from India

In this section, we first report the results for the potential impact of access to laptops through TFLS on the foundational math skills of students. This is then followed by an analysis of heterogeneous impacts of the policy across the dimensions of wealth status and gender. We then perform a variety of robustness checks to ensure that our double difference identification design is picking up the effect of the policy and not producing a spurious result.

Main findings

We report the results from our double difference identification design in Table 3. The results suggest that the potential exposure to the TFLS program had a positive effect on the foundational math proficiency of students. We, specifically, observe that the math scores are around 0.085 points higher for students who were potentially exposed to the program. This translates to an effect size of 2.3% when compared to the mean. The result implies that access to laptops can potentially help in improving basic foundational math skills of higher secondary students. We also observe in the dynamic double difference graph in Fig. 1 that our results are driven by improvement in foundational math proficiency of students in the years 2012 and 2014. This makes sense as the implementation of the TFLS program only began in September 2011. We also observe negligible effects for the year 2013, which might potentially be on account of the differential distribution cycle for the laptop program in different years.

We further assess the levels at which these learning improvements happen for mathematics when students get access to laptops. For this purpose, we estimate a linear probability model where our dependent variable now becomes a dummy which takes the value 1 if the student has achieved skill atleast at a certain level of learning in mathematics (Chakraborty and Jayaraman, 2019; Chatterjee and Poddar, 2021; Lahoti and Sahoo, 2020). This alternative formulation also has the advantage of addressing the issue of ordinality of math proficiency scores, which we use for our primary analysis. This is because the variable capturing proficiency scores is continuous in nature and can, therefore, be affected by the choice of scale. Using a linear probability model helps us to account for this concern as well.

Table 4 reports the results for this exercise to understand the levels of learning. We observe that the impact of access to laptops is much higher for higher levels of learning, such as subtraction and division, when compared to lower levels of learning. Students who were potentially exposed to the program were 5% (when compared to the mean) more likely to be proficient in subtraction when compared to students who were not exposed to the program. While the coefficient for division is imprecisely estimated, we still find that exposed students were 4.6% more likely to be proficient in it when compared to students not exposed to the policy. We do not find improvement in lower levels of learning, as the coefficients are much closer to zero.

Sub-sample analysis and heterogeneity

The education literature from India suggests that educational inequalities persist in the country in terms of gender, caste, religion, and economic status (Asadullah and Yalonetzky, 2012; Borooah, 2012; Desai and Kulkarni, 2008; Gandhi Kingdon, 2002; Kingdon, 2007; Varughese and Bairagya, 2020). Hence, it is possible that the heterogeneous effects of the Tamil Nadu Free Laptop program on math skills may exist based on beneficiary students’ individual attributes as well as social and religious affiliation. Unfortunately, our data does not provide us with information on the caste and religion of the student. In the next subsections, we therefore focus on the economic status as well as the gender of the student to understand potential impacts of the policy based on these attributes.

Economic status

Our reduced form analysis suggests that access to technological resources such as laptops can help to improve the math skills of students. As these resources are less affordable for students coming from resource-constrained households, the provision of free laptops to students from these backgrounds can have much larger impacts when compared to students coming from economically better-off households that might already have access to these resources. However, it is also possible that poor households receiving laptops consider it as a one-off economic opportunity to benefit from the sale of the asset. In this case, laptops will have much smaller, if any, impacts on students from these backgrounds.

The ASER data does not provide us with direct information on the economic status of the student. However, existing literature on India suggests that information on housing assets serves as a good proxy for the same (Chakraborty and Jayaraman, 2019). We, therefore, use data on housing quality to understand heterogeneity by the economic status of the student. Here, we focus on whether a student stays in a “Pucca house” or not, where “Pucca house” refers to durable houses made of burnt bricks and cement. We conjecture that a student living in a “Pucca house” is likely to be economically well off in a relative sense when compared to a student living in a “Kutcha or Semi-Pucca” house. Figure 2 plots the coefficients for sub-sample analysis for two different house types. We find that students not living in “Pucca house” and belonging to economically poorer households were the primary beneficiaries of the program in terms of their learning outcomes. Students living in “Pucca houses,” who were also likely to be much better off economically, experienced no positive effects of the TFLS program.

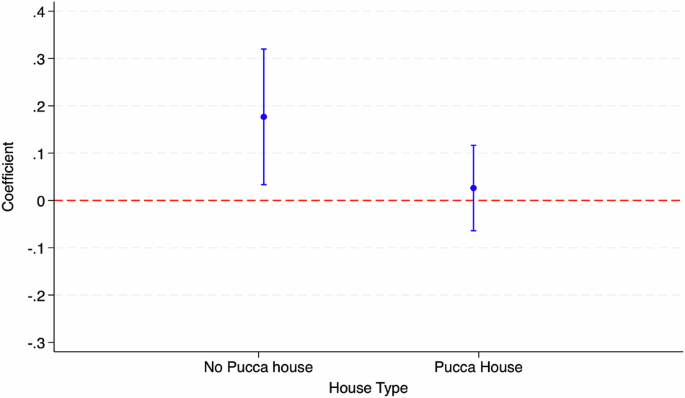
The figure shows sub-sample estimates (along with 95% confidence interval) for math proficiency for students residing in a “Pucca house” or “No Pucca house” using ASER data.

Gender

We then examine if access to laptops on account of the TFLS had any differential impacts on the math scores of boys and girls. Existing literature points towards differential use of computers for boys and girls that can potentially result in differential effects (Fairlie, 2016; Fairlie and Robinson, 2013). Also, in the Indian setting, where girls continue to experience educational disadvantage in school classroom settings, more focused and personalized access to resources through laptops has the potential to provide larger payoffs (Adukia, 2017; Chatterjee and Poddar, 2021; Gandhi Kingdon, 2002; Kingdon, 2007). Furthermore, if girls start from a lower base in math skills when compared to boys, the marginal impacts of access to laptops can be much higher for them. On the contrary, if boys start from a lower base, the marginal impacts for them are likely to be higher when compared to girls (Contini et al., 2017; Fryer and Levitt, 2010; Welmond and Gregory, 2021). The literature also suggests that in a resource-constrained setting, women and girls might be less likely to retain control over technological assets such as mobiles and laptops, as the control might pass on to a male family member or the asset might be sold off (Roessler et al., 2021). If that happens, improved access to laptops through TFLS will result in much lower average positive impact on the math skills of girls when compared to boys.

We, therefore, perform a sub-sample analysis for the potential impact of the program on the math skills of boys and girls in Table 5. As we can observe from the sub-sample analysis in Column (1) and Column (2), the math skills of both boys and girls seemingly improved on account of the TFLS. However, the coefficient for boys is almost double when compared to that of the girls. When we investigate further, we find that this difference in coefficient is indeed driven by economically constrained households not living in “pucca houses” (Table 6). Hence, it is possible that differential selling-off of laptops provided to girls by economically constrained households can potentially be one of the reasons for lower effects experienced by them. This also makes sense considering that anecdotal evidence on the policy from media reports suggests that several laptops distributed under the scheme do appear on the grey market; however, we do not have enough information on whether this was more prominent for girl beneficiaries.^{Footnote 21,Footnote 22}

Another potential factor that could have led to lower marginal positive effects on math scores for girls when compared to boys may be their higher starting base level in the subject. While evidence at the global level suggests that girls lag behind boys in math outcomes, evidence contrary to the same is also present for some countries and contexts.^{Footnote 23} (Contini et al., 2017; Fryer and Levitt, 2010; Welmond and Gregory, 2021). In the case of India, evidence indicates a gender gap in mathematics for predominantly North Indian States and, in contrast, a “reverse” gender gap where boys lag behind girls in predominantly South Indian states, including Tamil Nadu (Das and Singhal, 2023). Das and Singhal (2023) also rely on the ASER dataset for their analysis, as is the case in this study. When we look at our data, we find that boys (pre-policy mean math score = 3.790) studying in class 12th of government schools in Tamil Nadu lag behind in mathematics when compared to girls (pre-policy mean math score = 3.835) in the same cohort. Hence, higher positive impacts of the Tamil Nadu Free Laptop program for boys can also potentially reflect boys catching up with girls in terms of math scores, as they start from a lower base.

Robustness checks

Cohort falsification

Our double difference identification strategy relies on the use of cohort variation to pick out the effects of the TFLS program. Essentially, we are comparing the foundational math proficiency of students in class 12th (eligible cohort) with those in class 11th (ineligible cohort) and saying that in the absence of the program, the difference between the outcomes of these two cohorts would be zero. To test the validity of this identification assumption, we conduct a falsification check by comparing the outcomes of class 11th with those of class 10th students using the regression specification provided in Equation (1). Here, we provide a fake treatment to class 11th students and compare their outcomes to class 10th students. To do this, we generate a dummy variable “Class 11” which takes the value 1 if the student is in Class 11 of the government school and zero if student is in Class 10 of the government school. Since both these cohorts were essentially ineligible for the program, ideally, we should not find their foundational math skills to be statistically different from each other.

We report the results for this controlled experiment in Table 7 (Duflo, 2001). As expected, we do not find any statistical difference between the math learning outcomes of class 11th and class 10th students in Tamil Nadu. This gives us confidence that our double difference identification design is picking up the true causal effect of the TFLS program.

Alternative control group

We also try to test the sensitivity of our estimates to alternative definitions of the control group, i.e., the ineligible cohort. To do this, we now pool class 10 students and class 11 students together as a combined control group, i.e., the ineligible cohort, and compare their outcomes with the eligible treated group, i.e., class 12 students, before and after the program implementation in Tamil Nadu. The results for this exercise are reported in Table 8. As we can observe, the coefficients from the exercise are very similar to our main estimates, thereby providing us confidence that our identification strategy is correctly picking up the effect of the program.

Selection into government schools

A potential concern for our analysis is if the program altered the enrollment in government vis-a-vis private schools. This is possible as students might switch from private to government schools to gain access to program benefits. This has the potential to introduce selection bias in our results, as inclusion in our sample is conditional on a student studying in a government school. We, therefore, test if the introduction of the program impacted the likelihood of individuals enrolling in government vis-a-vis private schools and present our results in Table 9. The results suggest that the program did not have any impact on the likelihood of students enrolling in a government school when compared with a private school.

Alternative strategy: triple difference

In this section, we devise an alternative triple difference strategy to test the robustness of our results estimated using a double difference design (Gruber, 1994). Here, we introduce a third dimension to our existing double difference framework in the form of a state variation. This means that we now compare the foundational math proficiency of our eligible cohort (class 12th) to that of the ineligible cohort (class 11th) across our treated state of Tamil Nadu and other control states in India, before and after the program.^{Footnote 24,Footnote 25} Other than informing about the sensitivity of our main estimates, an additional advantage of using this alternative strategy is that it enables us to explore potential channels, using both ASER and IHDS datasets, through which the TFLS may impact foundational math skills. This is because it increases the statistical power and the precision with which we can pick the effects on account of a larger sample size accorded by the strategy. For instance, the data on English language competency that we explore as a potential channel is only available in the years 2009, 2012, and 2014. Similarly, the state-level sample in IHDS is quite small from the perspective of performing intra-state cohort-level analysis using a difference-in-difference design. The usage of the triple difference design here helps us to increase the precision with which we can pick out the effects of the TFLS on these intermediate variables that serve as potential channels for our effects.

In order to perform a triple difference analysis, we run the regression equation given below for each student i belonging to household h from village v in state s. As before, we restrict our analysis to students studying in government schools, as the scheme was only available to them.

In Equation (2), α_s and δ_t capture state fixed effects and time fixed effects, respectively. Treated is a dummy variable that takes the value 1 for the treated state of Tamil Nadu and zero, otherwise. Eligible and Post refer to dummies for the eligible cohort and post-policy period, respectively. Here, θ₁ is our coefficient of interest that picks out the effect of the TFLS program on the foundational math proficiency of students. We also use robust standard errors clustered at the state level for our analysis here.

Using Table 10 and Fig. 3, we first show that the parallel trends assumption for the triple difference model is satisfied (Muralidharan and Prakash, 2017). We then present the results from our triple difference design in Table 11. As can be observed, the results look very similar to our primary estimates using a double difference design. This gives us confidence that our primary strategy, based on a double difference design, is correctly picking the impacts of TFLS. As stated before, we use this triple difference design to study potential channels for our effects on foundational math proficiency in the next section.

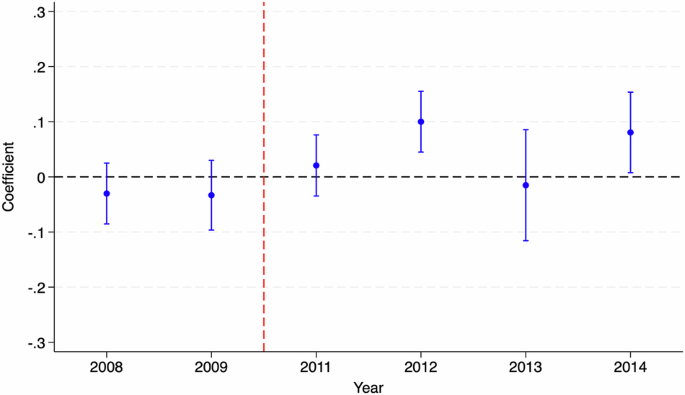
The figure shows dynamic triple difference estimates (along with 95% confidence interval) for Math Proficiency using ASER data. The year 2010 has been considered as the base year for the plot.

Other concerns and checks

A potential concern with our analysis is that the ASER data only covers students up to the age of 16 years to collect information on foundational math proficiency. While students aged 16 years were eligible to be enrolled in class 12th and constituted a significant proportion of enrolled students in the grade both in 2012 and earlier years in Tamil Nadu (NUEPA, 2013a, 2013b), this creates a concern in that we are missing out on students from upper age cohorts, e.g., 17–18 years of age, who might have also been enrolled in class 12th and may be characteristically different from students aged 16 years.^{Footnote 26} However, literature on the impact of age on learning outcomes suggests that this relationship is likely to be strong only in the early grades (Deming and Dynarski, 2008). Considering that we are looking at an outcome that is much below the grade level, the impact of the age of students studying in class 12th on our estimates is likely to be minimal. We further run a model, where we control for age fixed effects to account for time-invariant characteristics related to age. The results for this exercise are reported in Table 12 and are in line with our main estimates. We also conduct another check where we report estimates from a different specification where we cluster the standard errors at the district level and report the results in Table 13. As we can observe, the results are very similar to our main estimates and are robust to the use of bootstrap p values.